Trisecting the Angle

Bisecting an angle (splitting it into two equal ones) is not only possible, but also rather straightforward using a ruler and a compass. However, it is also well known that trisecting an angle using only the above instruments is impossible. This problem has an unexpected solution that requires no instruments but a single sheet of paper, using a method by Hisashi Abe that dates back to 1970s. The method goes as follows:

Step 1:
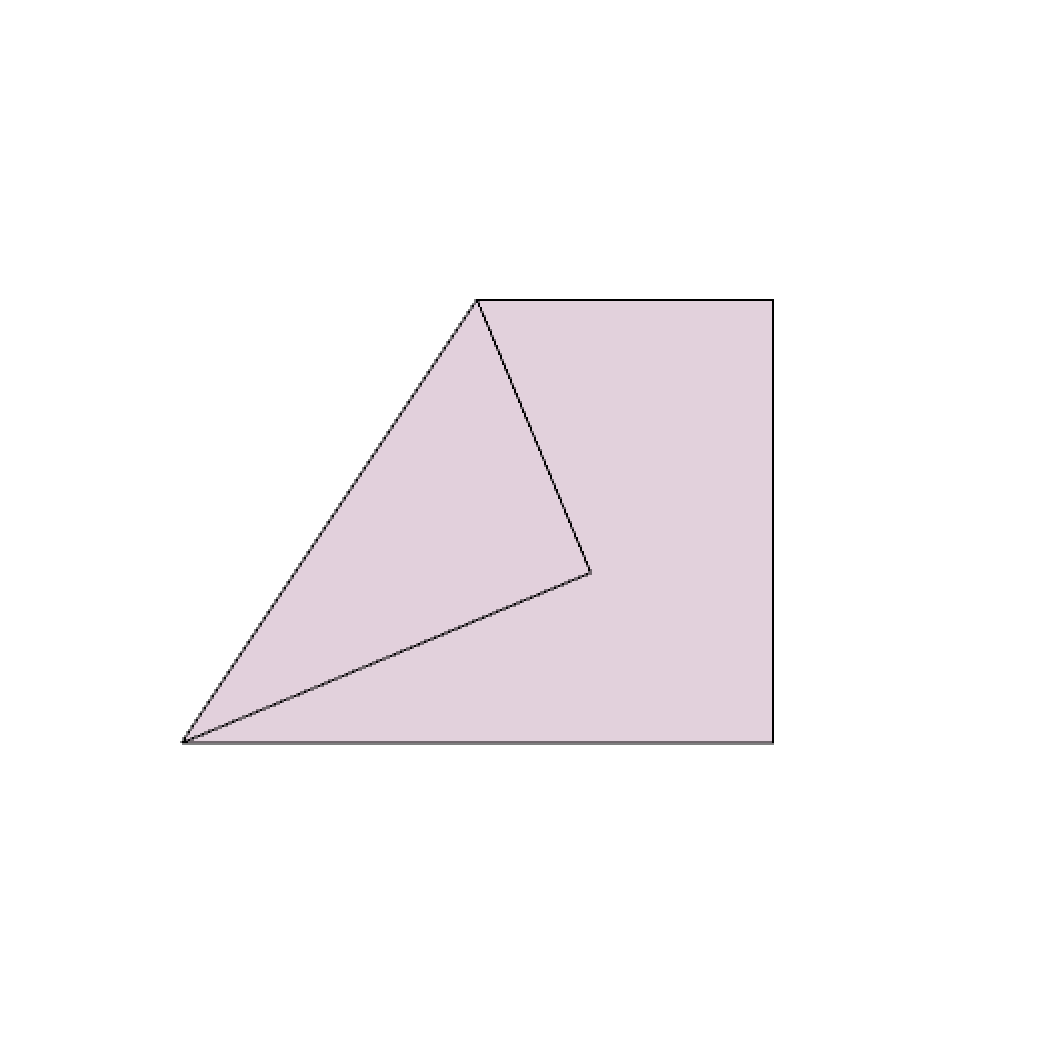
Fold the paper at an angle from the bottom left corner. That marks the angle that is desired to be trisected. This can be any acute angle, but note that if it is too small, some steps could go «out» of the paper and will be much harder to follow.

Step 2:
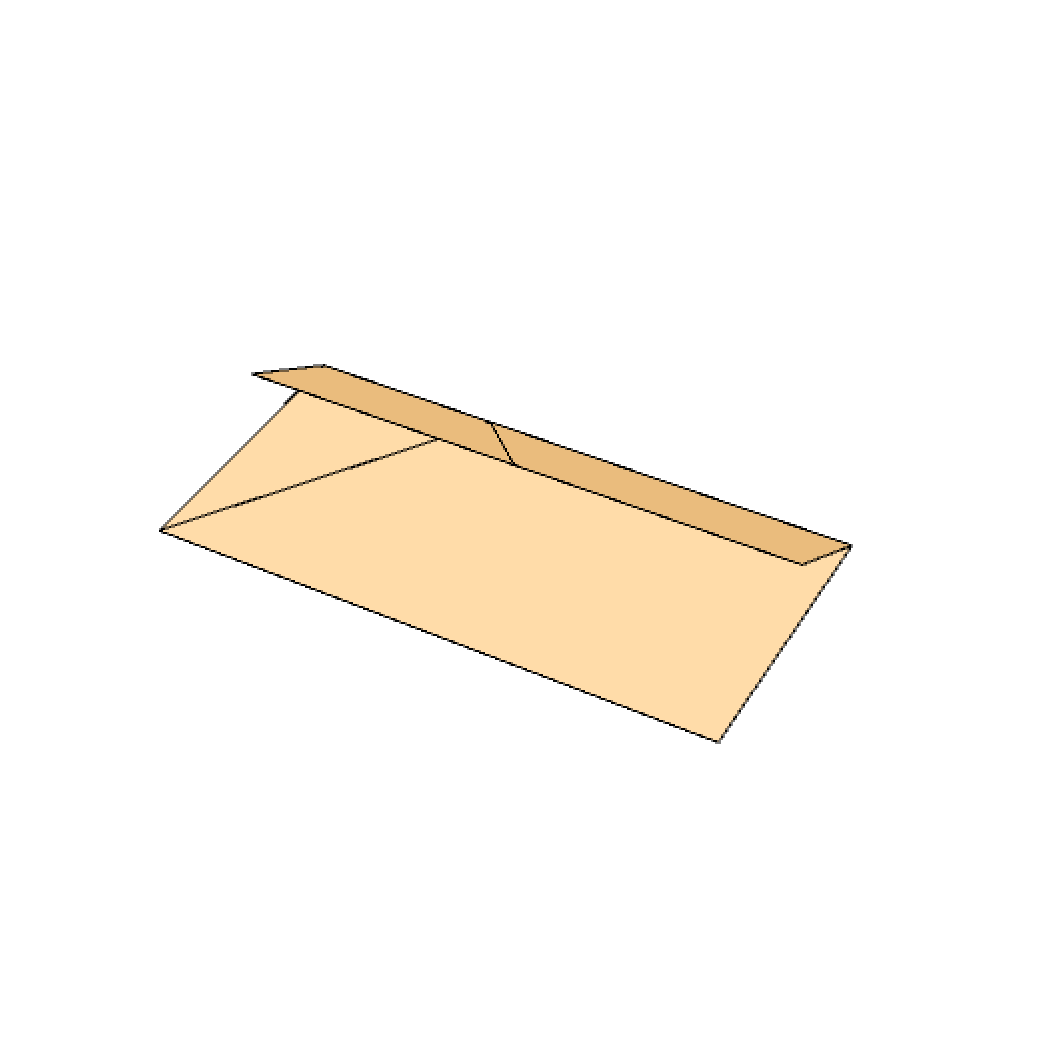
Fold the paper in parallel to the bottom side of the paper. The position of this fold is arbitrary, but has to be in the top half of the paper.

Step 3:
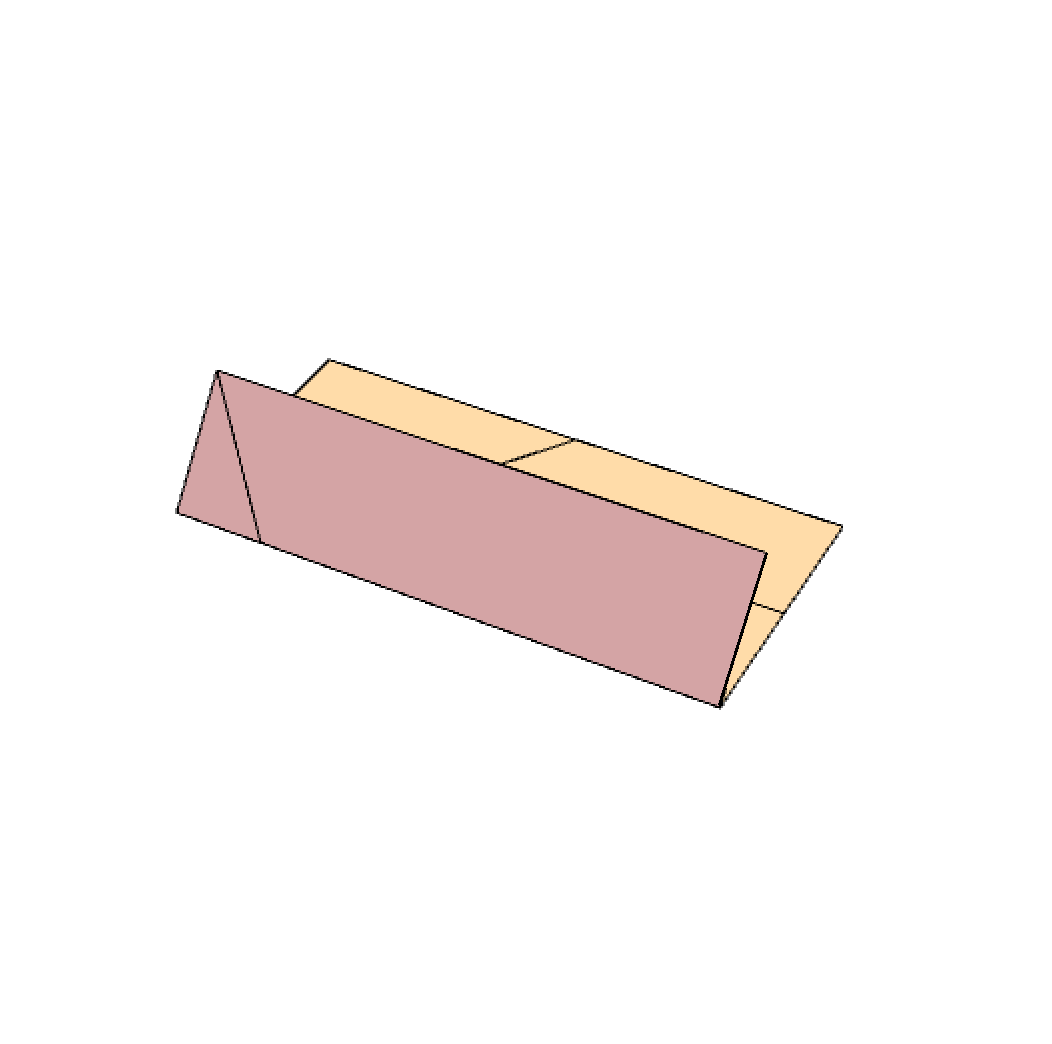
Create a second fold, parallel to the bottom of the page as well. This time, fold it in a way that a bottom of the paper lies on the crease fold created in the previous step.

Step 4:
This step can be tricky. You need to move two points onto two lines. First, the crease line created in step 2 (the top one parallel to the bottom side of the paper). You need to fold the paper such that its left end point lies on the crease line that defined the angle (in step 1). At the same time, after folding, the bottom left corner of the paper must lie on the crease line created in step 3 (the bottom one). See the figure below for clarity.

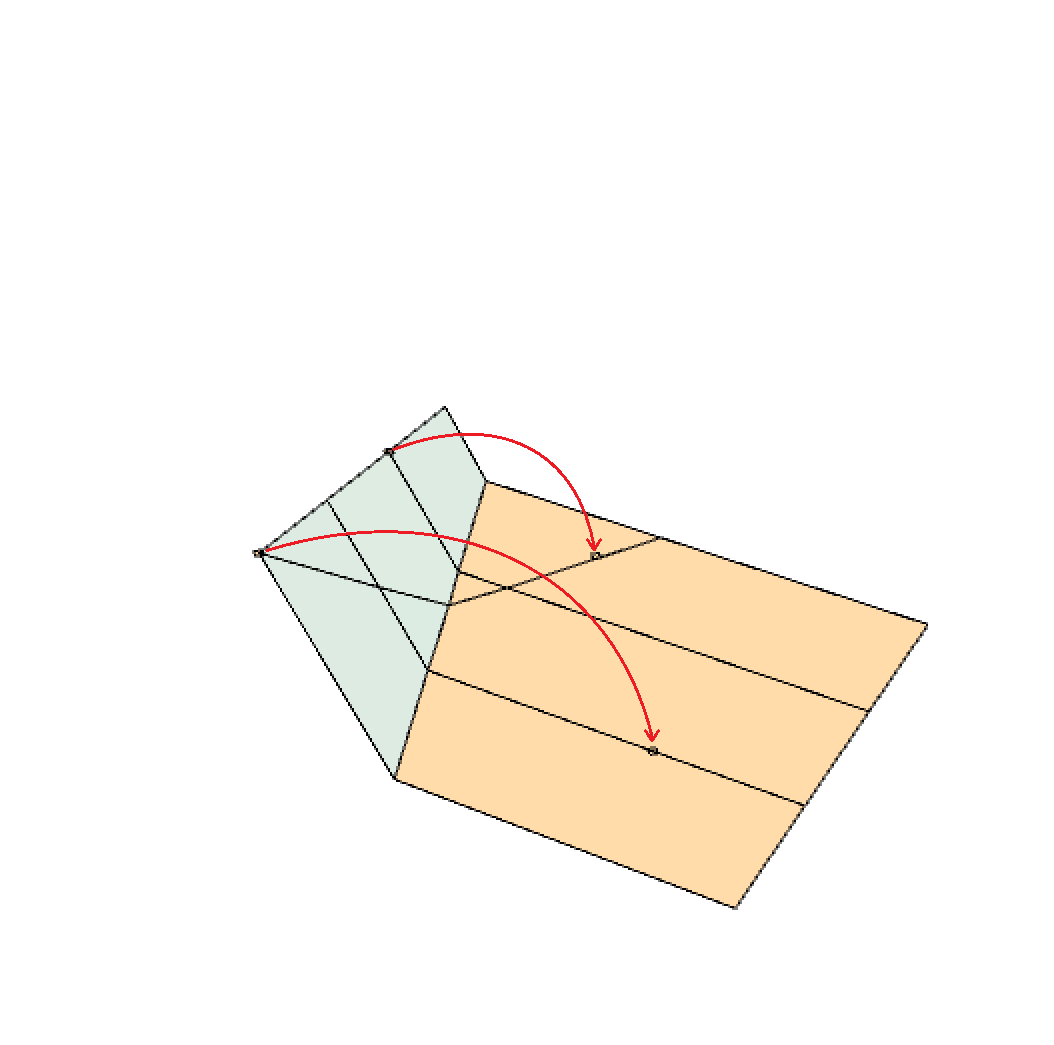
Step 5:
After you completed the fold in step 4, the continuation of the folded part of the bottom crease (created in step 3) can be marked extended to go across the entire paper, by either using a pen or by folding. This can be seen as the red line in the pictures below.

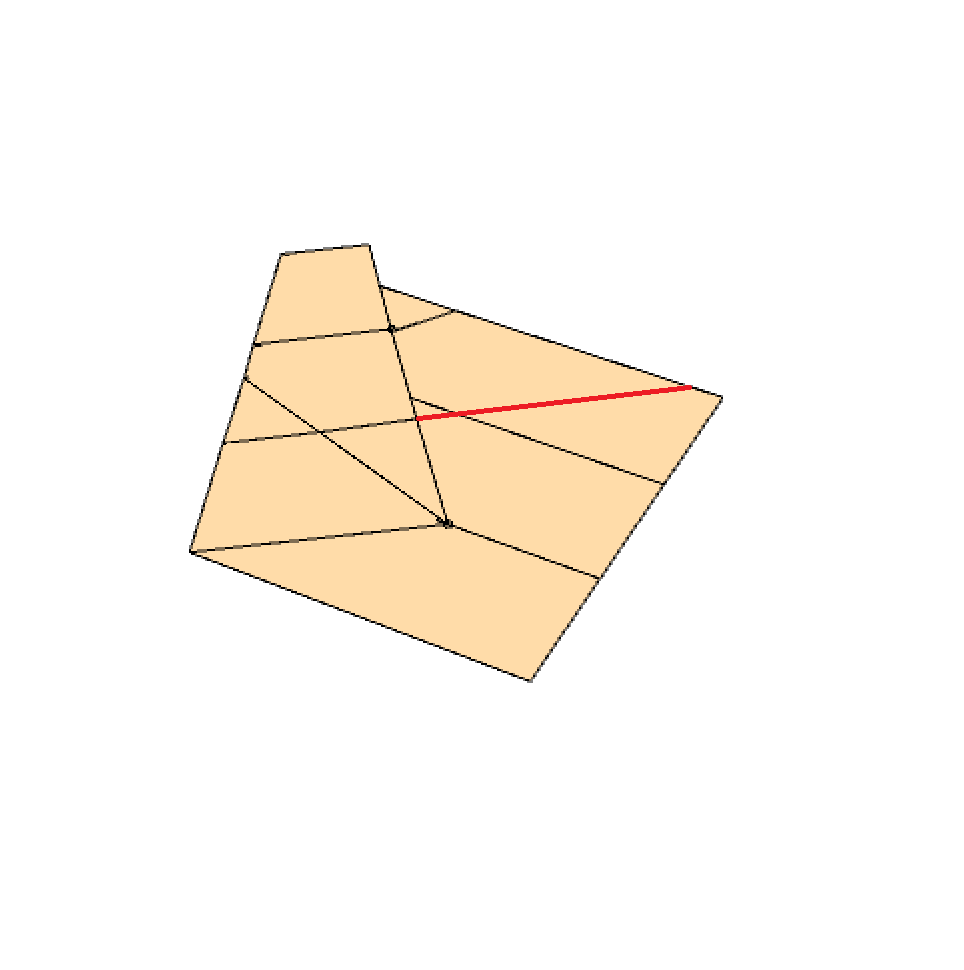
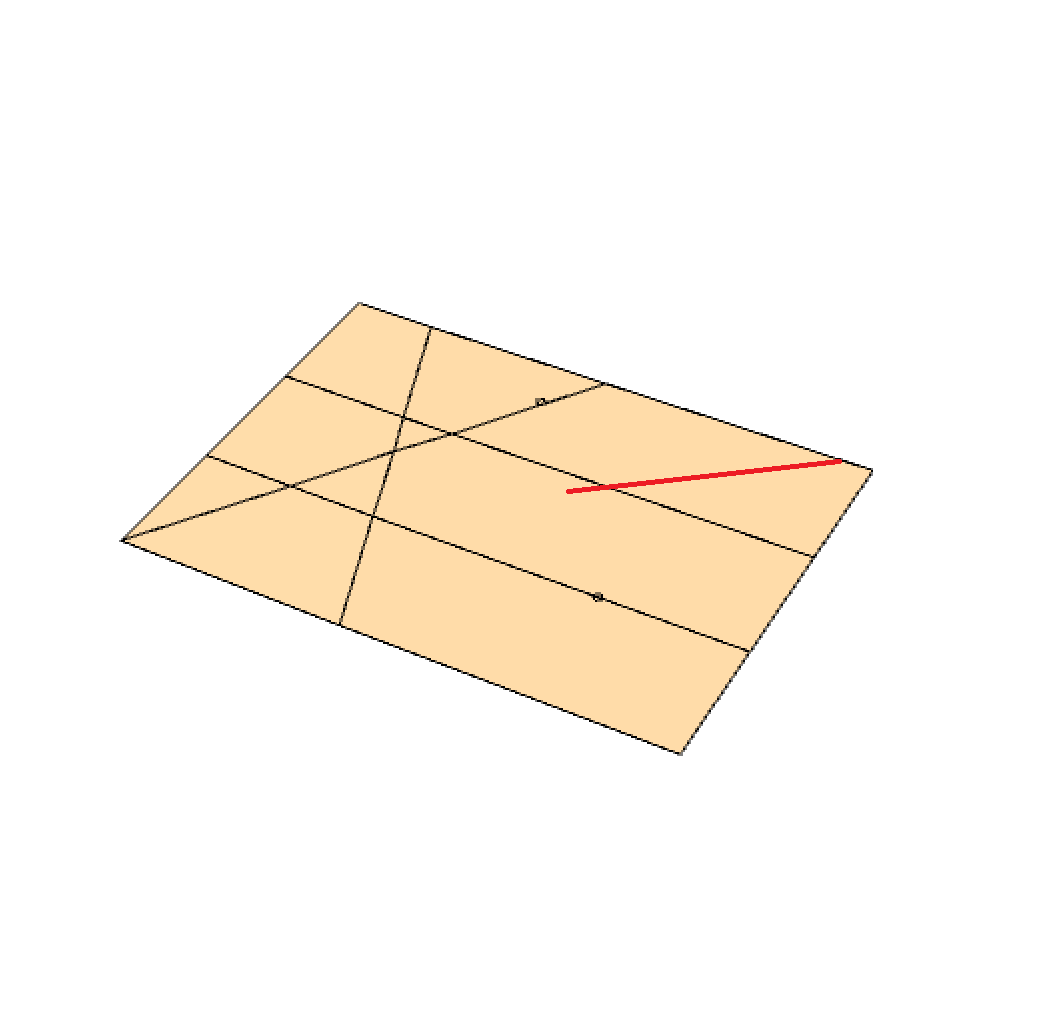
Step 6:
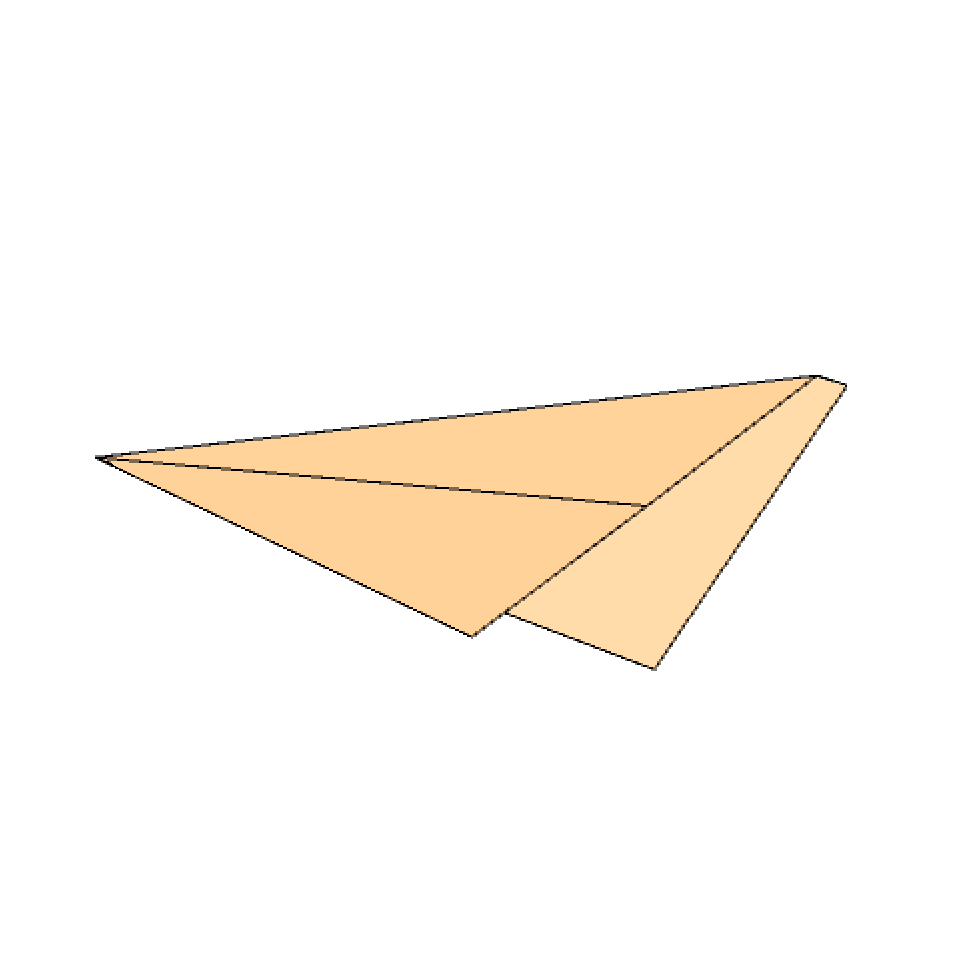
Lastly, take the bottom right corner and fold in a way that the bottom side of the paper lies on the crease pattern created in the previous step (found in step 5 and shown in red in the pictures above.

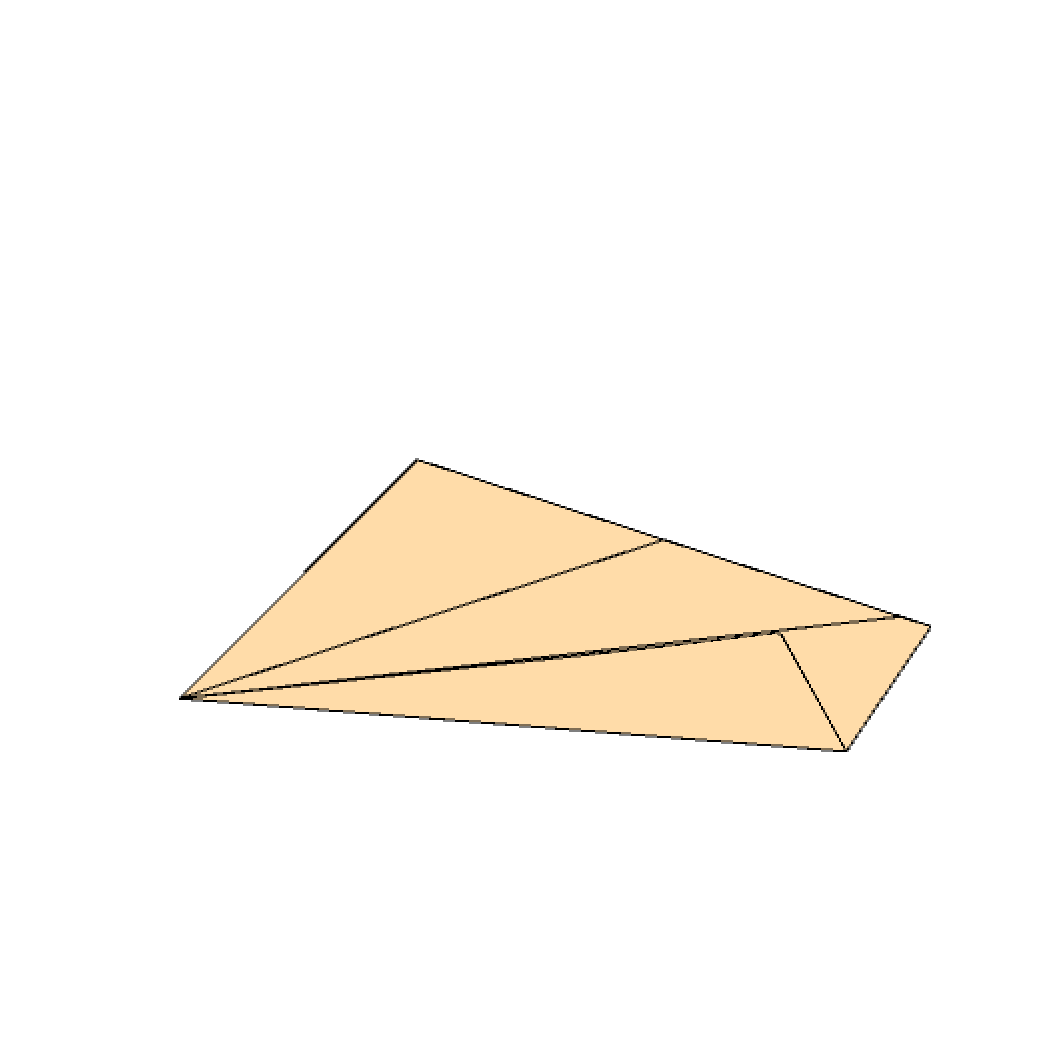
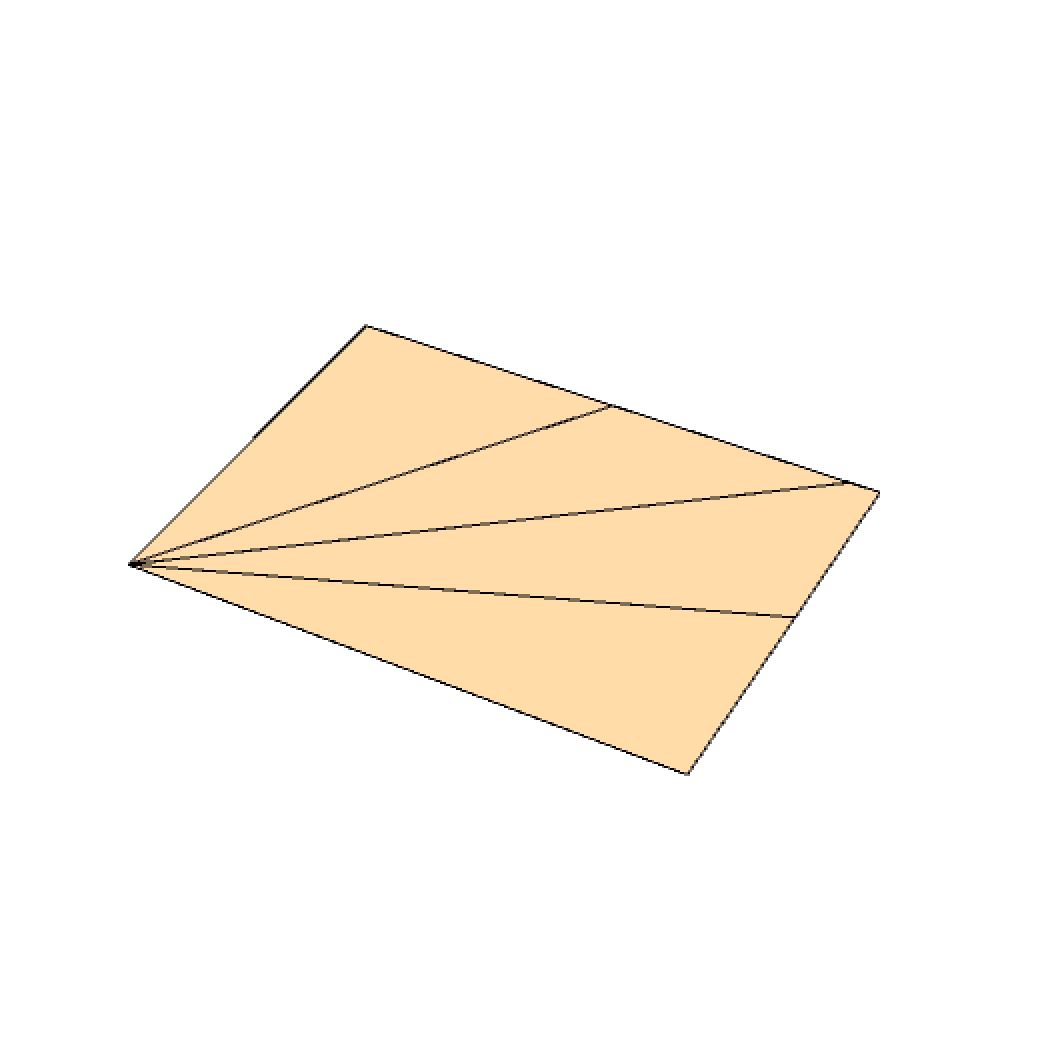
As a result, the required angle is split intro three equal parts as shown below.

If you are having trouble with this demonstration, you can see the full folding animation created in Wolfram Mathematica here: