Biggest Equilateral Triangle Inscribed in a Square

A typical mathematical problem of optimisation is to find the biggest equilateral triangle that fits inside a square. To do this demonstration, you need a square sheet of paper.

Step 1:
Fold the square in half along one of its sides and unfold it back, creating a crease line in the middle of the paper.

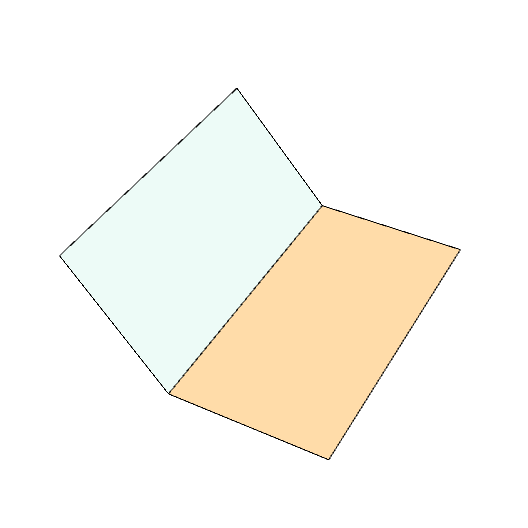
Step 2:
With the crease line aligned vertically, take the bottom right corner and fold the paper so that this corner lies on the vertical crease line. Mark the exact point where the corner ends up on the middle crease line. Unfold.

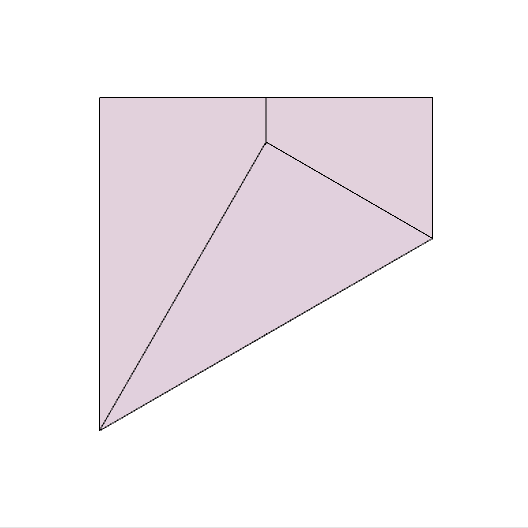
Step 3:
Take the top right corner and fold the paper such that this corner lies on the crease line created in step 2, AND the point marked in step 2 (shown as a rhombus on the pictures) lies on the crease line you are creating. Mark the point where the newly created crease intersects the top side of the square.

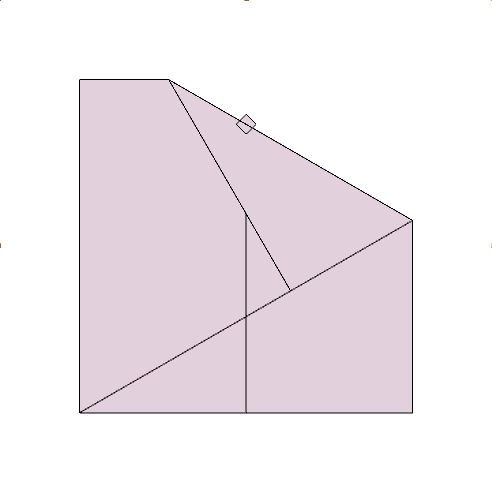
Step 4:
Take the bottom right corner again, this time fold the paper in a way that the bottom side of the square lies on the crease line created in step 2. Mark the point where this produced crease line meets the rights side of the square. Unfold.

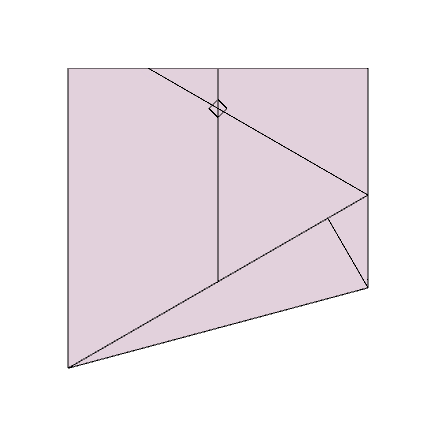
Step 5:
Take the top right corner and fold the paper such that the new crease line joins the point marked in step 3 to the rightmost point on the crease line created in step 4, then unfold this new crease.

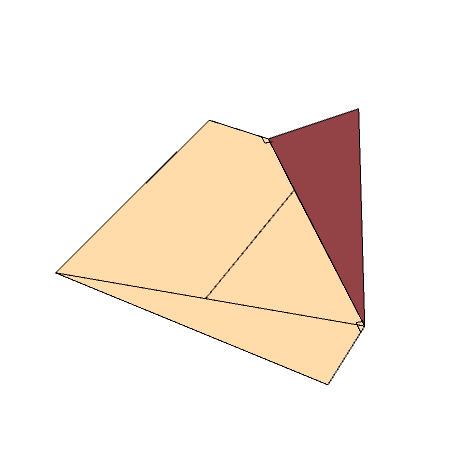
Step 6:
Finally, take the top left corner of the square and fold the paper so that the crease line connects the bottom left corner and the top end of the crease line created in step 5. Unfold.

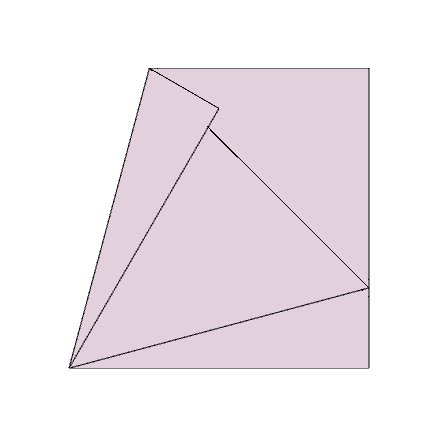
The triangle created this way is the biggest equilateral triangle that can possibly be inscribed into a square.

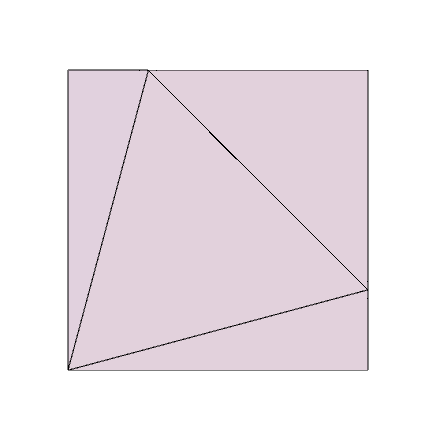
If you are having trouble with this demonstration, you can see the full folding animation created in Wolfram Mathematica here: