Doubling the Cube

Doubling the cube allows one to — given the length of the first cube edge — construct a second cube with double the volume of the first. The new cube has sides of length ∛2 times the original length. Incidentally, this construction cannot be solved using Euclidean methods. It can however be solved using paper folding demonstrated below. For this demonstration, you need a square sheet of paper.

Step 1:
The first step includes starting with a square paper and folding it along one of its sides into three equal parts, as shown below. To make it easier, you can you can do both folds simultaneously and make sure that all three parts lie on top of one another perfectly.

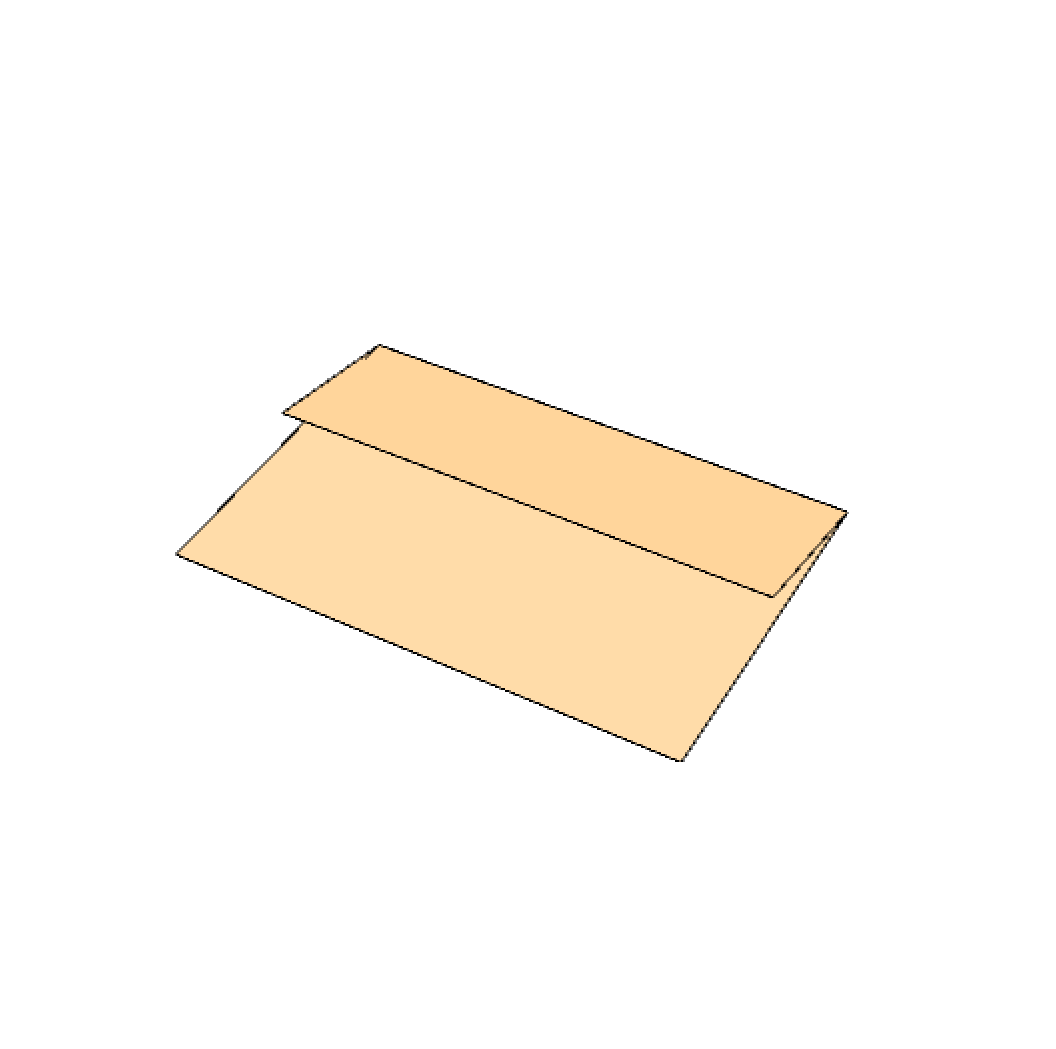
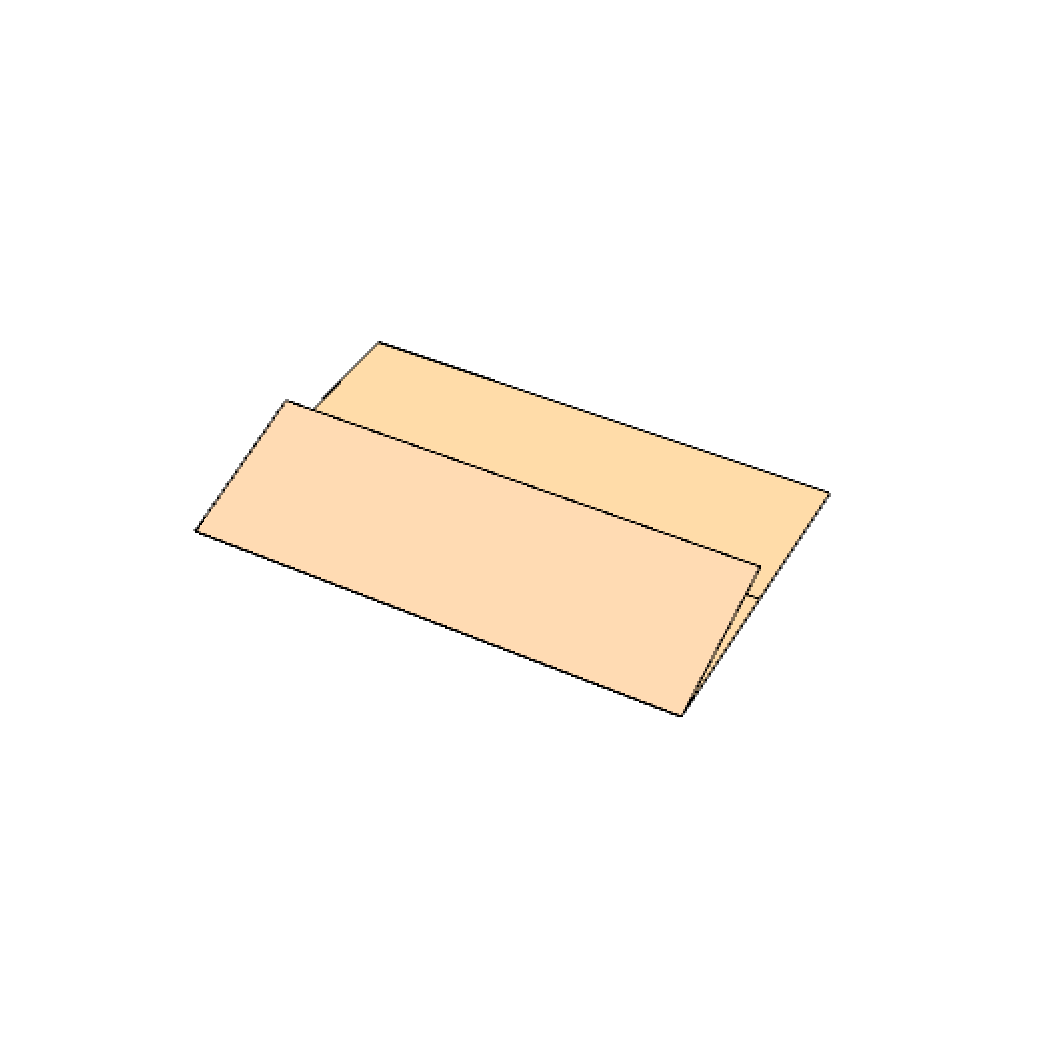
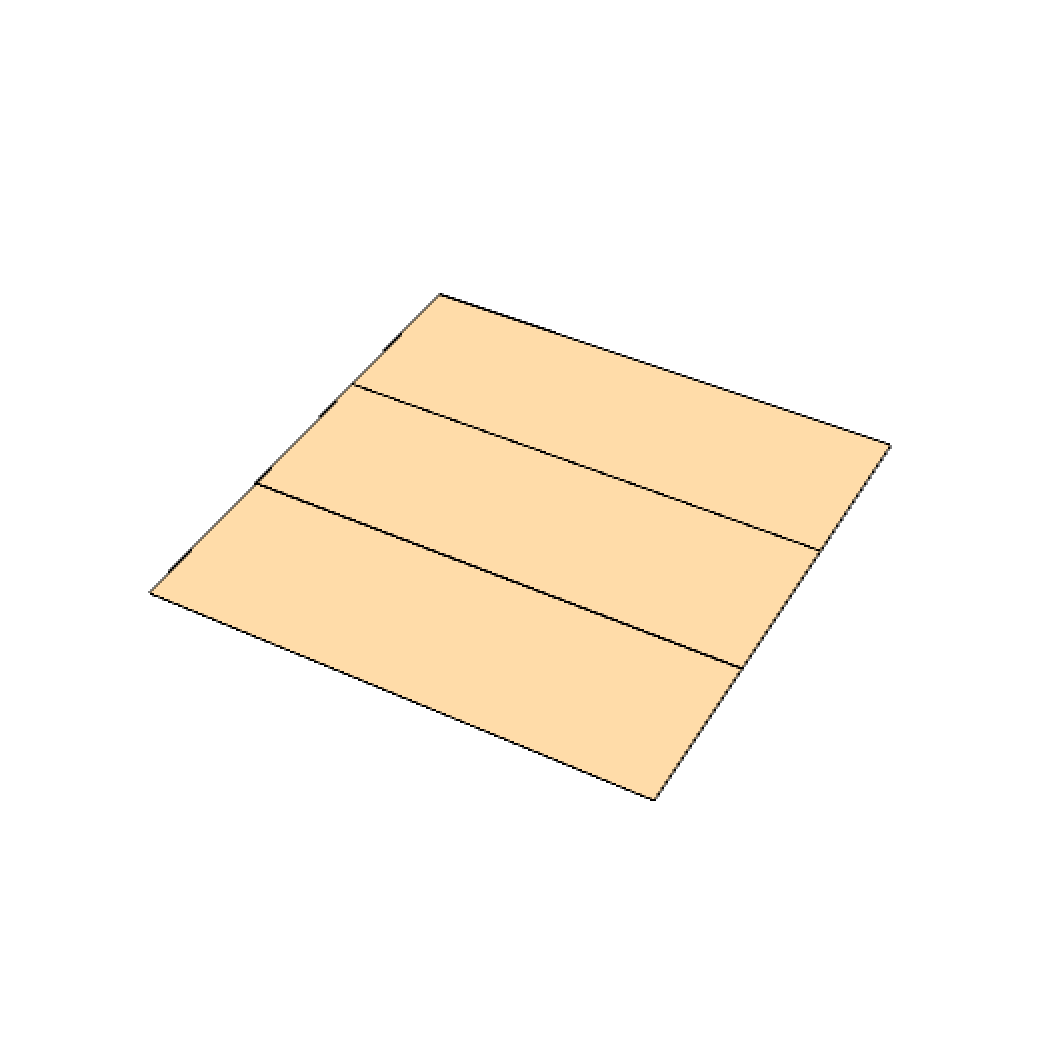
Step 2:
This step is pretty tricky. You need to fold the paper in such a way that the bottom left corner is brought to the right edge. Now look at the two crease lines created in step 1. You also need the left end point of the bottom crease line to lie on the top crease line. Mark the point where the bottom left corner ended up.

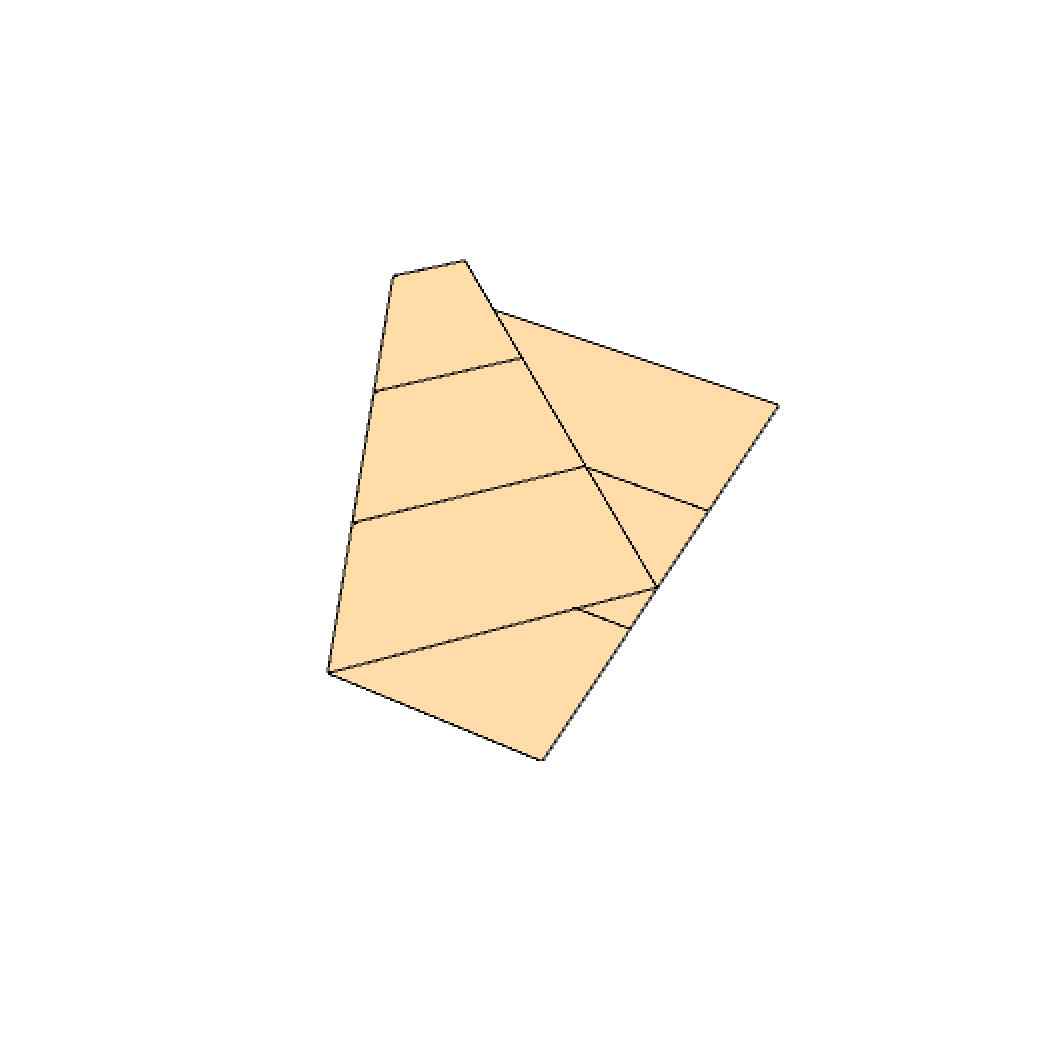
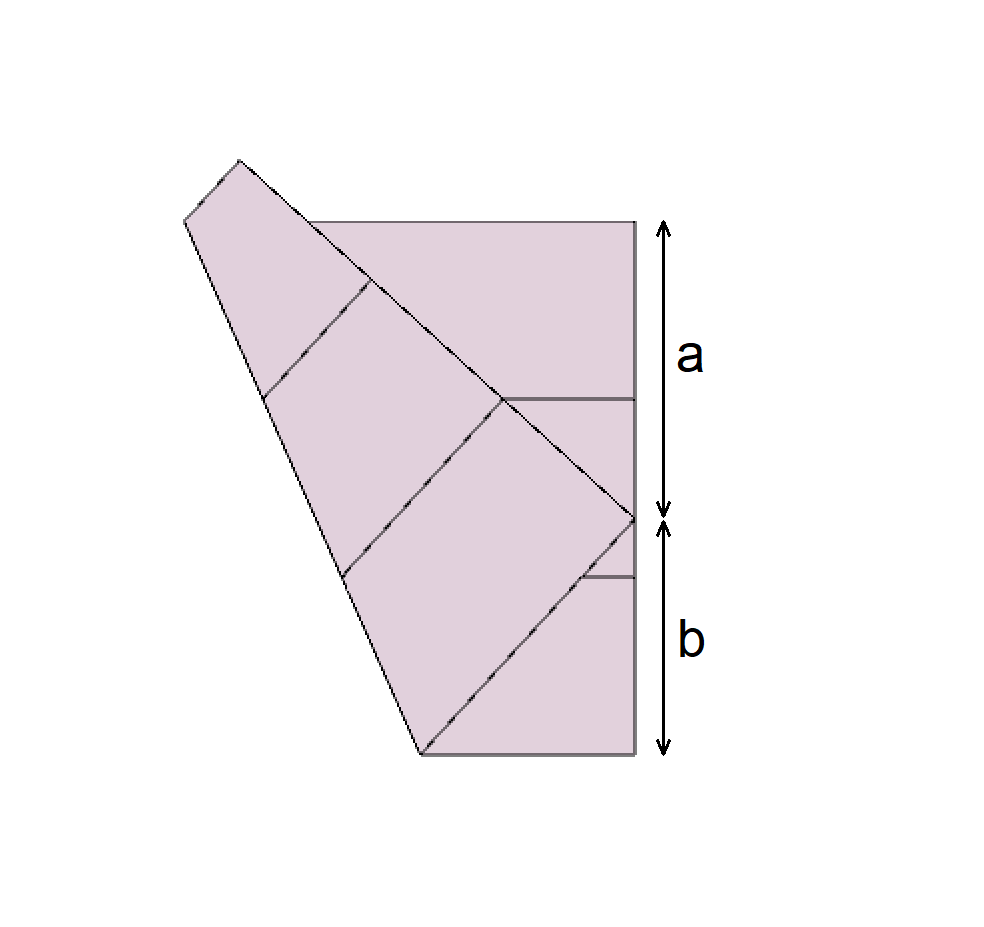
As a result, this new position of the bottom left corner divides the right-hand side of the square into two parts, a and b, in a way that the ratio ^a⁄_b=∛2, which is what we were looking for.

If you are having trouble with this demonstration, you can see the full folding animation created in Wolfram Mathematica here: